A mathematics modelling problem for you...
School Fundraising
Here we apply the modelling process to a very simple problem. The purpose is to illustrate aspects that are easily overlooked, but that are found in problems at all levels.
Problem:
A school plans a fundraising event, for which it has a sponsor and an equipment supplier. The sponsor agrees to pay an amount equal to 20% of the proceeds obtained, and the school agrees to pay the supplier 10% of the proceeds.
Does it matter whether the equipment supplier is paid before the sponsorship money is obtained – or vice versa?
We first consider the example simply as a problem with real-world connections.
Problem:
A school plans a fundraising event, for which it has a sponsor and an equipment supplier. The sponsor agrees to pay an amount equal to 20% of the proceeds obtained, and the school agrees to pay the supplier 10% of the proceeds.
Does it matter whether the equipment supplier is paid before the sponsorship money is obtained – or vice versa?
We first consider the example simply as a problem with real-world connections.
An approach to the problem...

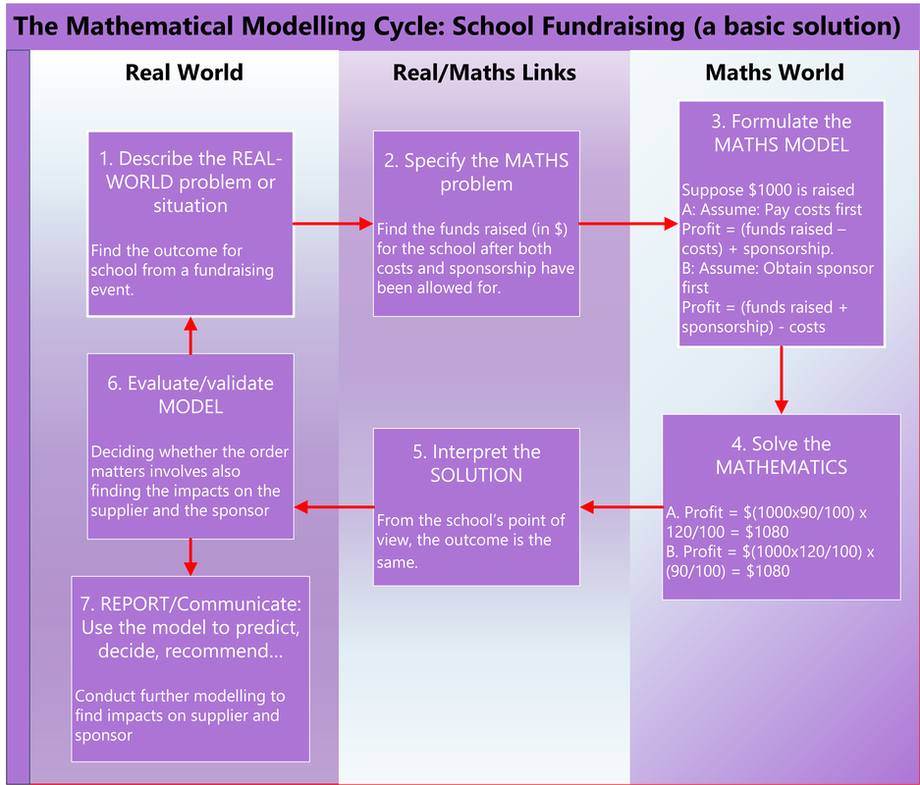
Suppose that the total takings are $1000.
A. Pay supplier first:
Amount to school after costs = $1000 x (90/100) = $900
Final amount to school= $900 x (120/100) = $1080
B. Obtain sponsors money first:
Amount to school after sponsor = $1000 x (120/100) = $1200
Final amount to school = $1200 x (90/100) = $1080
So, does the order matter?
From the school’s point of view... No ($1080 both ways).
From the viewpoint of the supplier and the sponsor... Yes!
A: Supplier gets $100 and Sponsor pays $180
B: Supplier gets $120 and Sponsor pays $200
In B, the sponsor has subsidised the supplier as well as sponsoring the school.
Here the problem has been treated as a one-off, for which a perfectly viable solution approach has been used.
There is, however, no suggestion that the problem might be seen as a member of a family of problem types, for which a common approach is applicable. An approach, which when learned, adds to the problem-solving armoury applicable for problems situated in real world contexts. That is a solution has been obtained, but without methodological growth.
We now approach the problem in ways that simultaneously obtain a solution and draw attention to a generic (modelling) process which provides a systematic methodology for a family of problems of which this is a very simple example.
To achieve this, we apply the modelling process illustrated below. This depiction of the modelling process doubles as scaffold for learners. The box labels indicate the kind of activity that will be undertaken and recorded systematically during different stages of the solution process. They give direction to the modelling and act as procedural referents. The box entries summarise main features within stages that will form the basis of a structured report.
1. A Basic Solution (illustrative not unique)
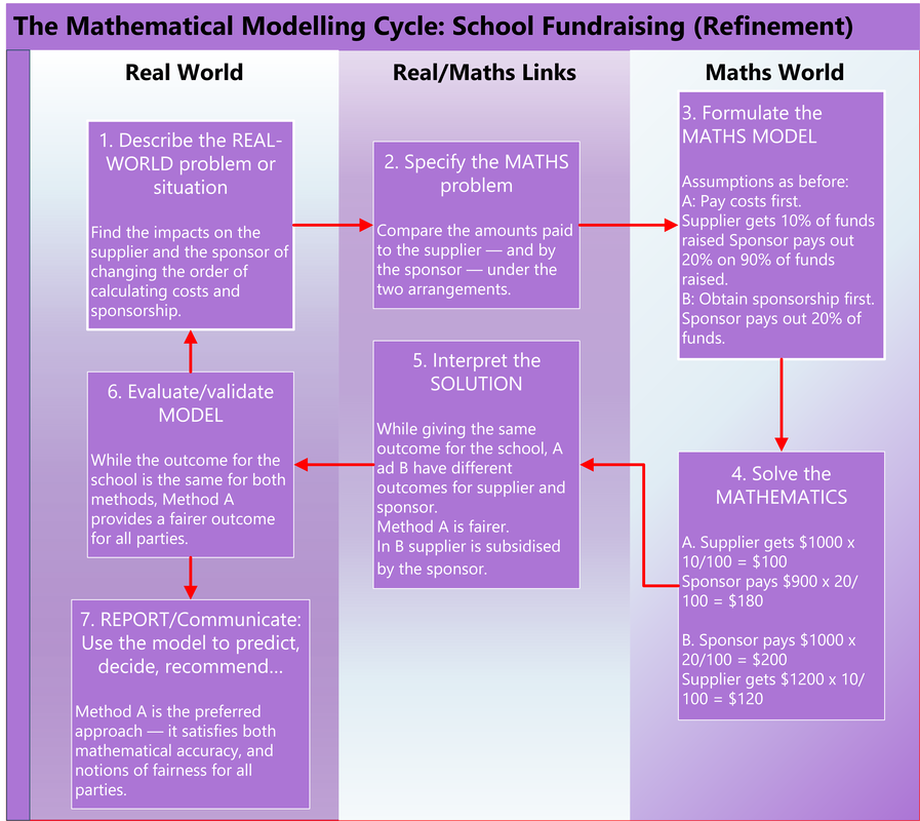
2. Refinement (interests of all parties included)
Again, the box headings provide structure for conducting the modelling process, and a report can be written by synthesising and elaborating the basic content generated within each stage.
For more complex problems, it may not be possible to contain all workings and ideas within the boxes, so box headings are usefully expanded to section headings under which solutions are developed and documented. This will be demonstrated for the "Is It Worth the Trip?" problem.
Organising a solution in terms of stages of the modelling process serves four purposes:
As noted earlier, there are different representations of the modelling process that involve cyclic activity in developing and refining the solution to a problem. The one used here is not definitive in some absolute sense. What it sets out to do in addition to depicting the modelling process, is to provide scaffolding assistance though stage headings that indicate the type of activity that needs to take place within respective phases of the modelling process.
In summary, teaching students how to model a problem set in the world outside the classroom is at a different level from giving students a problem with real-world connections and asking them to solve it. The first group has also been equipped with a systematic problem-solving method which the other lacks. In the words of John Rennie, when faced with a challenging new problem, one group has training to appeal to, and the other has not.
For more complex problems, it may not be possible to contain all workings and ideas within the boxes, so box headings are usefully expanded to section headings under which solutions are developed and documented. This will be demonstrated for the "Is It Worth the Trip?" problem.
Organising a solution in terms of stages of the modelling process serves four purposes:
- It makes us consciously aware that the solution of a real-world problem entails implementing sequential stages in a solution process — this can go unrecognised when we just collapse a solution to a simple problem mentally, or onto the back of an envelope.
- In writing down the detail of the solution in specific boxes, our attention is drawn to attributes that we might otherwise not recognise as key steps in modelling. For example, deciding whether to pay costs first or obtain sponsorship first, represent key assumptions that underpin the ultimate outcomes in this example. Corresponding features occur in all problems and it is important to get used to identifying and specifying them.
- The diagrammatic structure acts as a scaffold to assist in learning to model. As a concrete referent it relieves load on working memory for beginning modellers, who are simultaneously learning a process and solving a particular problem. With experience, the modelling process becomes internalised so that recourse to a physical representation is no longer necessary. When to do away with a scaffold is a decision for an individual modeller/learner.
- Internalisation of the modelling process becomes necessary as the demand and complexity of problems increase. For this example, skeletal entries indicate what is being accomplished within the different stages/boxes. As noted above, for more complex problems, solutions are too extensive to be written within boxes, but the headings of the latter, in addition to organising thinking, can become section headings in an elaborated project report. That is, consciously articulating the modelling process doubles as training for constructing systematic reports of a modelling project.
As noted earlier, there are different representations of the modelling process that involve cyclic activity in developing and refining the solution to a problem. The one used here is not definitive in some absolute sense. What it sets out to do in addition to depicting the modelling process, is to provide scaffolding assistance though stage headings that indicate the type of activity that needs to take place within respective phases of the modelling process.
In summary, teaching students how to model a problem set in the world outside the classroom is at a different level from giving students a problem with real-world connections and asking them to solve it. The first group has also been equipped with a systematic problem-solving method which the other lacks. In the words of John Rennie, when faced with a challenging new problem, one group has training to appeal to, and the other has not.
Modelling
|
Enablers
|
Members |