Let us set the scene...
It is important that students are able to use the mathematics they learn in school for purposes beyond those of their immediate courses.
Curriculum statements from a variety of well-respected sources emphasise this:
Australian Curriculum Assessment and Reporting Authority (2017)
Mathematics aims to ensure that students are confident, creative users and communicators of mathematics, able to investigate, represent and interpret situations in their personal and work lives and as active citizens.
OECD description of mathematical literacy
Mathematical literacy is an individual’s capacity to reason mathematically and to formulate, employ, and interpret mathematics to solve problems in a variety of real-world contexts. It includes concepts, procedures, facts and tools to describe, explain and predict phenomena. It (mathematical literacy) assists individuals to know the role that mathematics plays in the world and to make the well-founded judgments and decisions needed by constructive, engaged and reflective 21st century citizens.
U.S Common Core State Standards Initiative (2012)
Mathematically proficient students can apply the mathematics they know to solve problems arising in everyday life, society, and the workplace.
And...
Mathematically proficient students are comfortable making assumptions and approximations to simplify a complicated situation, realizing that these may need revision later. They are able to identify important quantities in a practical situation and map their relationships using mathematical tools They can analyze those relationships mathematically to draw conclusions, and routinely interpret mathematical results in the context of the situation, and reflect on whether the results make sense…
The bottom line…
When confronted with a crisis, you will not rise to the occasion, you will sink to the level of your training.
John Rennie when Editor of the Scientific American
What Rennie is stressing is the importance — indeed the necessity — of specialised training if individuals are to be equipped to meet the challenges that arise in a chosen field of activity.
So, why Mathematical Modelling?
One of the best ways to acquire the ability to apply mathematics learnt in the classroom to solve problems in the world beyond the classroom, is to successfully engage in the process of mathematical modelling. Yet you’ll see this term does not appear in any of those curriculum statements.
This is not entirely a bad thing because the term mathematical modelling has been given a variety of meanings in education, many of which have little or nothing to do with developing abilities to solve problems that emerge in real life.
It is this goal — to solve real-life mathematical problems, implicit in the foregoing curriculum statements — that characterises our work. The main aim of mathematical modelling is to develop abilities that will not be achieved elsewhere in the mathematics curriculum.
Our approach is consistent with that put forward by Niss et, al. (in their 2007 book on the study of Applications and Modelling in Education, sponsored by the International Commission on Mathematical Instruction).
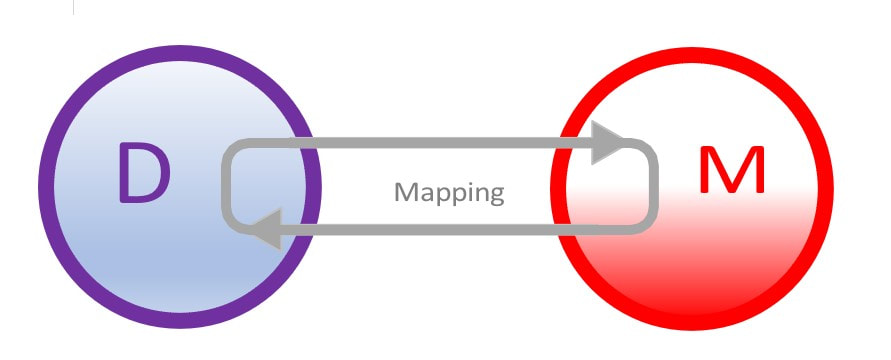
In this approach, problems identified in the “extra-mathematical domain” — in other words, the “real world” — are mapped into the “mathematical domain” — where models, theories, solutions are proposed — before being translated or mapped back into the “extra-mathematical domain” for validation.
The figure below shows this process:
This is not entirely a bad thing because the term mathematical modelling has been given a variety of meanings in education, many of which have little or nothing to do with developing abilities to solve problems that emerge in real life.
It is this goal — to solve real-life mathematical problems, implicit in the foregoing curriculum statements — that characterises our work. The main aim of mathematical modelling is to develop abilities that will not be achieved elsewhere in the mathematics curriculum.
Our approach is consistent with that put forward by Niss et, al. (in their 2007 book on the study of Applications and Modelling in Education, sponsored by the International Commission on Mathematical Instruction).
In this approach, problems identified in the “extra-mathematical domain” — in other words, the “real world” — are mapped into the “mathematical domain” — where models, theories, solutions are proposed — before being translated or mapped back into the “extra-mathematical domain” for validation.
The figure below shows this process:
D: Extra-mathematical domain
M: Mathematical domain
Mapping: From D to M and translated back to D
M: Mathematical domain
Mapping: From D to M and translated back to D
The extra-mathematical world is a useful way of representing that part of the wider "real world" that is relevant to a particular problem.
By real world we mean everything that is to do with nature, society, or culture, including everyday life, as well as school or university subjects and subject areas other than mathematics.
This extra-mathematical domain includes contexts such as workplace, citizenship, and personal problem solving, as referred to in the curriculum statements.
Objects, relations, questions, etc. within the extra-mathematical domain (D) are identified and selected as relevant for a particular modelling purpose and situation. These are then mapped (or translated) into corresponding objects, relations, questions, etc. within the mathematical domain (M).
Within M, mathematical deliberations, manipulations and inferences are made.
These outcomes are then translated back to D and interpreted within the extra-mathematical domain.
This modelling cycle may be iterated several times, as deliberations, manipulations and inferences are validated and evaluated, until the resulting conclusions concerning the extra-mathematical domain are satisfactory.
By real world we mean everything that is to do with nature, society, or culture, including everyday life, as well as school or university subjects and subject areas other than mathematics.
This extra-mathematical domain includes contexts such as workplace, citizenship, and personal problem solving, as referred to in the curriculum statements.
Objects, relations, questions, etc. within the extra-mathematical domain (D) are identified and selected as relevant for a particular modelling purpose and situation. These are then mapped (or translated) into corresponding objects, relations, questions, etc. within the mathematical domain (M).
Within M, mathematical deliberations, manipulations and inferences are made.
These outcomes are then translated back to D and interpreted within the extra-mathematical domain.
This modelling cycle may be iterated several times, as deliberations, manipulations and inferences are validated and evaluated, until the resulting conclusions concerning the extra-mathematical domain are satisfactory.
To see how the model is expanded and applied to the classroom, please go to our Mathematical Modelling Cycle page.
Modelling
|
Enablers
|
Members |