So, what is the Mathematical Modelling Cycle?
As mentioned in our introduction to mathematical modelling, problems identified in the real world are mapped across to the mathematical domain to be formulated and solved before being transferred back to the extra-mathematical domain for validation and evaluation.
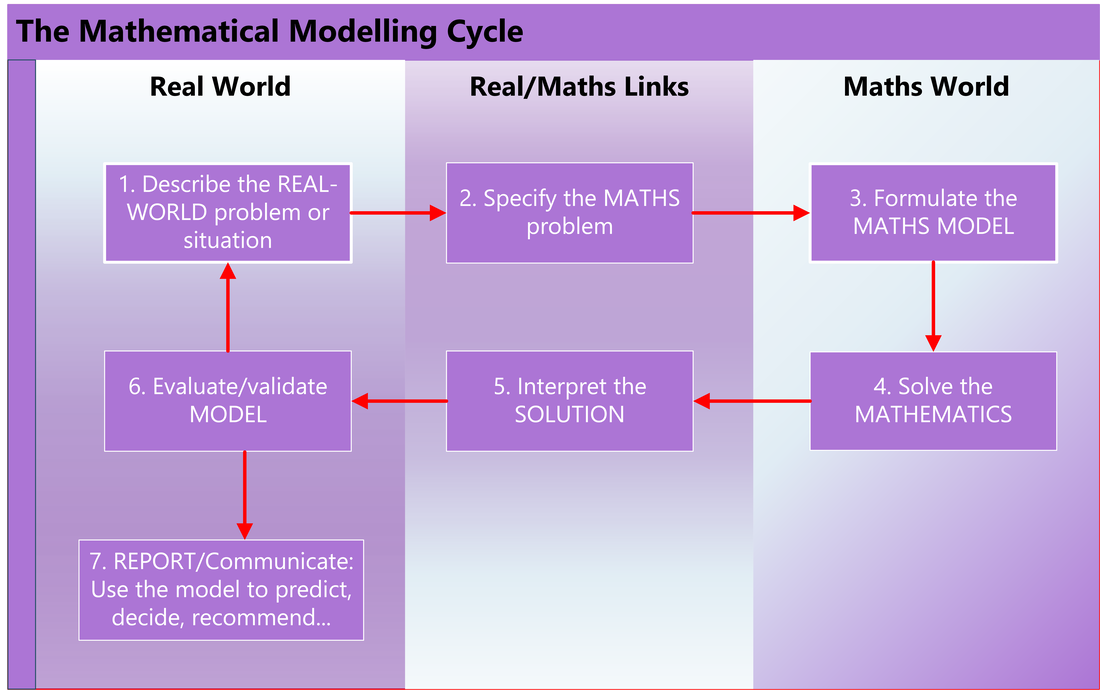
The modelling cycle can be further sub-divided into components, each describing essential elements and their order in the modelling process.
As you can see from the diagram below, the first column focuses on the "real world" or the extra-mathematical domain. The third column relates to the mathematical world. The middle column represents the interface between the real world and the mathematical world.
There are seven components to the mathematical modelling cycle in the representation below:
The modelling cycle can be further sub-divided into components, each describing essential elements and their order in the modelling process.
As you can see from the diagram below, the first column focuses on the "real world" or the extra-mathematical domain. The third column relates to the mathematical world. The middle column represents the interface between the real world and the mathematical world.
There are seven components to the mathematical modelling cycle in the representation below:
*The process illustrated in the diagram is consistent with the description given by Pedley
(President of the Institute of Mathematics and its Applications),
in describing how mathematics is applied to solve real problems.
(President of the Institute of Mathematics and its Applications),
in describing how mathematics is applied to solve real problems.
THE SEVEN COMPONENTS OF THE CYCLE*:
1. IDENTIFY and DESCRIBE a real-world problem or situation
A problem context is identified in the "real world". By “real world” we mean everything that is to do with nature, society, or culture, including everyday life, as well as school or university subjects, and subject areas different from mathematics. The real world is sometimes also described as the extra-mathematical domain. It can include contexts such as workplace, citizenship, and personal problem solving, as referred to in the curriculum statements.
Objects, relations, questions, etc. within this extra-mathematical domain are identified and selected as relevant for a possible modelling purpose and situation.
From the above activity several specific problems of interest may be suggested. The next task is to identify a problem, whose solution will involve mathematics, and be the focus of the modelling to come.
For example, the general context might be a change in taxation rates. A specific question to be addressed through modelling might be to find the impact of the rates change on a particular family — whose structure could be chosen individually or collectively by students. Alternatively, it could be to compare the impact on families in different circumstances.
Objects, relations, questions, etc. within this extra-mathematical domain are identified and selected as relevant for a possible modelling purpose and situation.
From the above activity several specific problems of interest may be suggested. The next task is to identify a problem, whose solution will involve mathematics, and be the focus of the modelling to come.
For example, the general context might be a change in taxation rates. A specific question to be addressed through modelling might be to find the impact of the rates change on a particular family — whose structure could be chosen individually or collectively by students. Alternatively, it could be to compare the impact on families in different circumstances.
2. SPECIFY the mathematical problem
The extra-mathematical problem is then mapped (or translated) into the mathematical domain.
How can the problem be re-interpreted as a mathematical problem — or problems — to be solved?
What objects, relations, questions, can be identified within the mathematical domain?
A specific question needs to be stated in the form it is to be modelled.
For example:
Find the impact of taxation rate changes on a family of four (with two dependent children), on a single income of $75 000 per year.
An extra-mathematical problem has been made specific to the extent that in can now be mapped (or translated) into the mathematical domain.
How can the problem be re-interpreted as a mathematical problem — or problems — to be solved?
What objects, relations, questions, can be identified within the mathematical domain?
A specific question needs to be stated in the form it is to be modelled.
For example:
Find the impact of taxation rate changes on a family of four (with two dependent children), on a single income of $75 000 per year.
An extra-mathematical problem has been made specific to the extent that in can now be mapped (or translated) into the mathematical domain.
3. FORMULATE a mathematical model
What objects, relations, questions, can be identified within the mathematical domain that support an approach to a solution?
In other words, what mathematical deliberations, manipulations and inferences can be made? What mathematical processes can be employed?
These will involve making assumptions, selecting necessary variables, and choosing (and perhaps researching) values of parameters (constants) that will feature in solution processes.
Sometimes more than one approach is possible, and looking forward can be helpful in deciding which is more accessible, or suitable.
In other words, what mathematical deliberations, manipulations and inferences can be made? What mathematical processes can be employed?
These will involve making assumptions, selecting necessary variables, and choosing (and perhaps researching) values of parameters (constants) that will feature in solution processes.
Sometimes more than one approach is possible, and looking forward can be helpful in deciding which is more accessible, or suitable.
4. SOLVE the mathematics
Mathematical deliberations, manipulations and inferences are made as a solution is developed. Sometimes a choice of technology can assist the solution process.
5. INTERPRET the solution
This is a crucial step in mathematical modelling where the models, theories, solutions proposed are translated back to the real-world context.
This represents a mapping from the mathematical domain back into the extra-mathematical domain.
This represents a mapping from the mathematical domain back into the extra-mathematical domain.
6. EVALUATE/VALIDATE the model
Can the deliberations, manipulations, inferences and resulting conclusions be validated in terms of the outcomes they generate for the extra-mathematical domain?
That is, can the solution be evaluated as satisfactory in terms of the real-world context? Has the modelling done its job?
If not, the modelling process should be repeated or refined, circling back to earlier stages of the cycle.
That is, can the solution be evaluated as satisfactory in terms of the real-world context? Has the modelling done its job?
If not, the modelling process should be repeated or refined, circling back to earlier stages of the cycle.
7. REPORT the findings
When the evaluation of the model within the real-world context has taken place with a satisfactory outcome, the findings should be communicated.
This report can take various forms and will include any recommendations arising from the solution to the problem.
It should include a description of the designated problem, a full account of the solution process, and a discussion of the outcome, including justification for its acceptance.
A report may be conveniently structured by making use of the respective headings of the phases in the modelling cycle. Its content should be extensively covered by the cumulative documentation of progress within the successive phases.
This report can take various forms and will include any recommendations arising from the solution to the problem.
It should include a description of the designated problem, a full account of the solution process, and a discussion of the outcome, including justification for its acceptance.
A report may be conveniently structured by making use of the respective headings of the phases in the modelling cycle. Its content should be extensively covered by the cumulative documentation of progress within the successive phases.
To download an A4 version of the modelling cycle, please click HERE.
*It should be noted that the mathematical modelling cycle as shown in the diagram represents the problem-solving process rather than the solution paths of individuals. These can vary widely in detail (involving to and fro movement between the stages) as errors and deficiencies are identified and corrected.
Modelling
|
Enablers
|
Members |